- Beauty
It is a scientific truism known to modern humans that the earth is round, so how round is the earth? The answer given by scientists is that the earth is so round that it can be described as a near-perfect sphere.

This raises some doubts, because there are great undulations on the surface of the earth, upwards of 8,000m high mountains and downwards of 10,000m deep ocean trenches, if this is the case, why do scientists still say that the earth is very round?
A wrong view
There is a belief that the reason the earth looks round is because of the earth's oceans, which simply means that a lot of seawater "Fills in" The undulations on the surface of the earth. The following oft-quoted image seems to confirm this view.
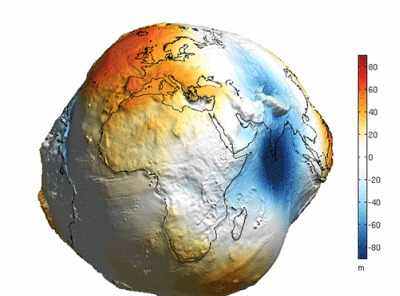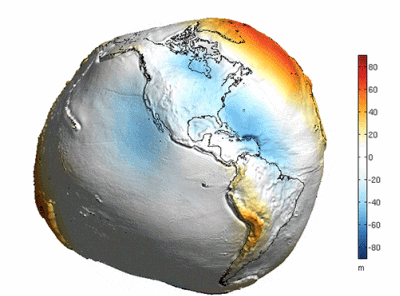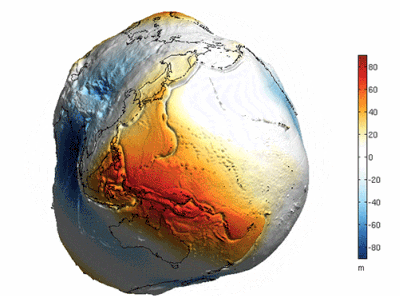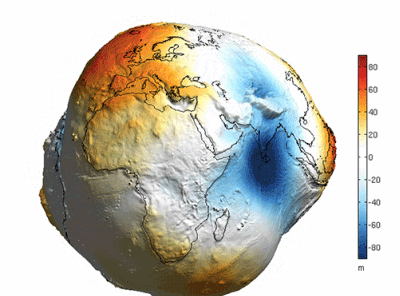
Is this really the case? The answer is no. Because this picture is a very exaggerated depiction of the difference in height of the "Geoid" (i.e. The gravitational isotope that coincides with the rest of the sea level), and not the "Earth as it would be if all the water were pumped out of it".
If you look closely you will see that the quantities in the scale on the right hand side of the graph range from plus or minus 80 in 'm', or 'metres', which compares to the earth's radius of about 6371 km, the difference in height of the 'geoid "Compared to the earth's radius of about 6,371 km, the difference in height of the "Geodetic level" Is several orders of magnitude smaller than the earth's radius, so to speak, scientists have chosen to exaggerate the difference in order to represent it more visually.
Scientists say that the earth is round, but this is an objective description of the earth
It is true that the earth has trenches more than 10,000 metres deep and mountains more than 8,000 metres high. The known data show that mount everest is the highest mountain on earth, with an altitude of about 8,848 metres, and that the deepest trench on earth is the mariana trench, with a depth of 11,034 metres, which is indeed very considerable for mankind, but compared to the volume of the earth, it is nothing.

The average radius of the earth is about 6371 km. A simple calculation shows that the height of the earth's highest mountain is equivalent to only about 0.14% of the earth's radius, while the depth of the earth's deepest trench is equivalent to about 0.17% of the earth's diameter - what a concept!
Let's put it this way, the radius of a standard basketball is about 123 mm, which means that if we were to reduce the earth to the size of a standard basketball, the highest bump on the earth's surface would be about 0.17 mm and the lowest depression would be about 0.2 mm, with a height difference of only 0.37 mm, which is shallower than the depth of the grain on a basketball, which can be considered quite flat.

Of course, the flatness of the surface does not indicate that the earth is round, but what really determines to what extent the earth is round is actually the error of the earth's roundness on the whole.
The earth is always rotating and in the process generates a 'centrifugal force', a virtual force whose magnitude is proportional to its angular velocity, and on the surface of the earth, the lower the latitude the greater the angular velocity and the greater the 'centrifugal force', which causes the earth to this causes a degree of bulging at the earth's equator, making the earth's polar radius larger than the earth's equatorial radius.
In the past, scientists have measured the earth's data via satellites, and the measured data shows that the earth's polar radius is about 6356.8 km and the equatorial radius is about 6378.1 km, a difference of 21.3 km, which gives an overall circularity error of "21.3/(6356.8 + 6378.1)/2". 6378.1)/2", which is calculated to be about 3.3‰ (3.3 parts per thousand).

As a comparison, a good quality table tennis ball with a diameter of 40 mm used for tournaments requires that the roundness error is controlled to within 0.1 mm, which is 5‰ (5 parts per thousand), which means that if we reduce the diameter of the earth to 40 mm, then its roundness error will be perfectly in line with the standard of a good quality table tennis ball.
The analysis of the above data shows that the earth can indeed be said to be very round. In fact, the images of the earth actually captured by us humans through various spacecraft are indeed the same, and the earth will always be presented in a near-perfect spherical shape when viewed from space.

What exactly is the force that makes the earth so round in shape?
The answer is gravity. Of the four fundamental forces known in the universe, gravity is the weakest, and because it is a long-range force and has only an 'attractive' force and no 'repulsive' force, it can be superimposed indefinitely.
We know that the magnitude of gravity is proportional to mass, so that when an object reaches a certain mass, its own gravitational force can be superimposed enough to cause the matter that makes up the object to behave as a fluid at the macroscopic level.
As long as the mass of the object is large enough, even if the object is composed mainly of rocky material, in which case the object will naturally evolve into a sphere-like shape when the material that makes up the object reaches hydrostatic equilibrium.